Header
Message
Zamanın Yamulması
Evrenin Zarafeti - Brian Greene \ Zamanın Yamulması
Einstein, kütleçekimini anlamak için aşırıya varan, neredeyse takıntılı bir yoğunlukla çalışıyordu. Bern’deki patent bürosunda, o isabetli fikre ulaşmasından beş yıl sonra fizikçi Arnold Sommerfeld’e şu satırları yazmıştı: “Bugünlerde sadece kütleçekimi sorunu üzerinde çalışıyorum. (....) Şurası kesin ki, hayatımda hiçbir şey beni bu kadar yormamıştı. (....) Bu problemle karşılaştırılınca orjinal [özel] görelilik kuramı çocuk oyuncağı gibi kalıyor.”
Öyle görünüyor ki bir sonraki kilit atılımı, özel göreliliği kütleçekimi ile ivmeli hareket arasındaki bağa uygulamanın getirdiği basit fakat kolayca anlaşılmayan sonuca ulaşması 1912’de gerçekleşecekti. Einstein’ın mantık yürütmesindeki bu adımı anlayabilmenin en kolay yolu, tıpkı onun yaptığı gibi, belli bir ivmeli hareket örneğine odaklanmaktan geçer. Bir cismin hızı ya da hareket doğrultusu değiştiğinde ivmelendiğini hatırlayalım. Basit olması için, cismimizin hızı sabit kalırken sadece hareket doğrultusunun değiştiği ivmeli harekete odaklanalım. Özellikle de, lunaparkta Tornado’ya bindiğinizde yaşanana benzer, bir çember şeklindeki hareketi düşünelim. Tornado’ya binip duruşunuzun sağlamlığını hiç sınamadıysanız şöyle anlatayım, sırtınızı yüksek hızda dönen dairesel pleksiglas yapının iç kısmına dayayarak durursunuz. Bütün ivmeli hareketlerde olduğu gibi, bu hareketi hissedersiniz; vücudunuzun merkezden dışa doğru çekildiğini, dairesel pleksiglas duvarın sırtınıza baskı yaptığını, sizi bir daire izleyecek şekilde hareket eder halde tuttuğunu hissedersiniz. (Aslına bakarsanız, buradaki tartışmayla ilgili olmasa da belirteyim, dönme hareketi sizi pleksiglasa öyle bir kuvvetle “çiviler” ki, üzerinde durduğunuz çıkıntı olmasa da aşağıya doğru kaymazsınız.) Hareketiniz hiç sarsıntısızsa, gözlerinizi kapattığınızda, sırtınızdaki baskı –tıpkı bir yatağın desteği gibi- neredeyse yatıyormuşsunuz gibi hissetmenize yol açar. “Neredeyse” lafı, olağan “dikey” kütleçekimini hala hissetmenizden, dolayısıyla beyninizin tümüyle kandırılamamasından gelir. Fakat Tornado’ya dış uzayda binecek olsanız ve Tornado doğru hızda dönecek olsa, dünyada hareket etmeyen bir yatağa uzanmışsınız gibi hissedersiniz. Dahası, “ayağa kalkıp” dönen pleksiglasın iç yüzeyinde yürüyecek olsanız, ayaklarınız pleksiglasa yere basıyormuş gibi basardı. Aslına bakarsanız uzay istasyonları da bu şekilde dönüp dış uzayda suni bir kütleçekimi duygusu yaratacak şekilde tasarlanmışlardır.
Dönen Tornado’nun ivmeli hareketini kütleçekimini taklit etmek için kullandığımıza göre, artık Einstein’ı takip edip uzay ve zamanın bu alete binen birine nasıl göründüğünü incelemeye geçebiliriz. Einstein’ın akıl yürütmesi bu duruma uyarlandığında şu şekilde ilerliyordu: Biz, duran gözlemciler dönen Tornado’nun çevresini ve yarıçapını kolaylıkla ölçebiliriz. Örneğin çevreyi ölçmek için, Tornado’nun dönen kısmının etrafını bir cetvelle, cetveli kaydıra kaydıra ölçeriz; yarıçapını ölçmek için de aynı yöntemi kullanarak Tornado’nun ortasından dış duvarına doğru ilerleriz. Lise geometrisinden hatırladığımız gibi, çevresiyle yarıçapının oranının, pi sayısının iki katına eşit olduğunu buluruz –yaklaşık 6,28- tıpkı bir kağıt üzerine çizilen bütün dairelerde olduğu gibi. Peki ya Tornado’nun içindeki birine işler nasıl görünecektir?
Bunu öğrenebilmek için, Tornado’da dönüşün keyfini çıkaran Slim ile Jim’den bizim için birkaç ölçüm yapmalarını istiyoruz. Cetvellerimizden birini çevreyi ölçsün diye Slim’e, diğerini de yarıçapı ölçmesi için Jim’e veriyoruz. Durumu rahatça değerlendirebilmek için, Tornado’ya aşağıdaki şekilde görüldüğü üzere yukarıdan bakalım.

Tornado’nun bu çizimini, hareket doğrultusunu gösteren bir okla süsledik. Slim çevreyi ölçmeye başladığında, onu yukarıdan izlerken, bizim bulduğumuzdan daha farklı bir sonuca ulaşacağını hemen anlıyoruz. Cetvelini Tornado’nun çevresini ölçmek için yere koyduğunda, cetvelin boyunun kısaldığını fark ediyoruz. II.Bölüm’de tartıştığımız, bir cismin hareket doğrultusundaki boyutunun kısalmış görünmesine yol açan Lorentz büzülmesinden başka bir şey değil bu. Cetvelin daha kısa olması, Slim’in Tornado’nun çevresini ölçebilmek için, cetveli daha fazla kere yere koyması gerektiği anlamına geliyor. Slim cetvelinin hala 30 santimetre uzunluğunda olduğunu düşündüğünden (Slim ile cetveli arasında göreli bir hareket olmadığından, cetvelini hala normal uzunluğunda gibi algılıyor), bu durum, Slim’in ölçümüne göre, Tornado’nun çevresinin bizim ölçtüğümüzden daha uzun çıkacağı anlamına geliyor.
Peki ya Tornado’nun yarıçapı? Jim de merkezden çevreye doğru uzanan kirişi ölçerken aynı yöntemi kullanıyor, onu yukarıdan izlerken bizim bulduğumuz sonuca ulaşacağını görüyoruz. Bunun sebebi, cetveli Tornado’nun hareket doğrultusuna paralel kullanmasıdır (oysa çevrenin ölçümünde durum böyle değildi). Cetvel hareket doğrultusuyla 90 derecelik bir açı yapacak şekilde kullanılmaktadır, bu yüzden de boyu kısalmamıştır. Dolayısıyla Jim, bizim bulduğumuzla tıpatıp aynı bir yarıçap uzunluğuna ulaşacaktır.
Fakat Slim ile Jim, Tornado’nun çevresinin yarıçapına oranını hesapladıklarında bizim bulduğumuz cevaptan (pi sayısının iki katı) daha fazla bir sayı bulacaklar, çünkü çevreyi daha uzun, ama yarıçapı aynı uzunlukta ölçtüler. İşte bu biraz tuhaf. Nasıl olur da şu dünyada daire şeklinde bir şey, Eski Yunanlıların farkına vardığı bütün dairelerde bu oranın pi sayısının tam iki katı olacağı kuralını çiğner.
İşte Einstein’ın açıklaması: Eski Yunanlıların vardığı sonuç, düz bir yüzeye çizilmiş daireler için geçerlidir. Fakat nasıl bir lunaparktaki güldüren aynalar yansımanızın normal uzamsal ilişkilerini çarpıtıyorsa, yamulmuş ya da eğri bir yüzeye çizilen dairenin olağan uzamsal ilişkileri de çarpılır: Çevresinin yarıçapına oranı genellikle pi sayısının iki katı olmaz.
Aşağıdaki şekillerde yarıçapları birbirinin aynı olan üç daire kıyaslanmaktadır. Fakat dairelerin çevrelerinin aynı olmadığına dikkat edin.
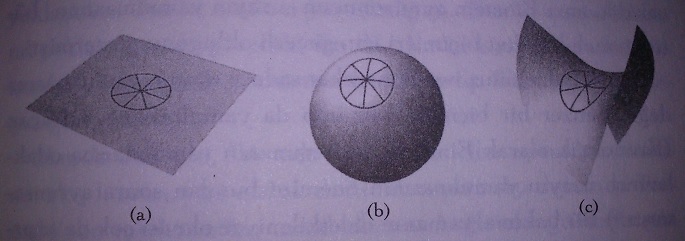
Bir kürenin eğri yüzeyine çizilmiş olan dairenin çevresi, a’daki düz bir yüzeye çizilmiş dairenin çevresinden kısadır, ama ikisinin de yarıçapı aynı uzunluktadır. Kürenin yüzeyinin eğri yapısı, dairenin merkezinden geçen çizgilerin biraz birbirine yaklaşmasına, sonuçta da dairenin çevresinin biraz küçülmesine yol açar. Yine eğri bir yüzeye –eyer şeklindeki bir yüzeye- çizilmiş olan, c’deki dairenin çevresi ise düz bir yüzeye çizilmiş olan dairenin çevresinden uzundur; eyerin yüzeyinin eğri yapısı, dairenin merkezinden geçen çizgilerin birbirinden biraz uzaklaşmasına, sonuçta da dairenin çevresinin biraz uzamasına yol açar. Bu gözlemler, b’deki dairenin çevresinin yarıçapına oranının pi sayısının iki katından az olacağı, aynı oranın c’deki pi sayısının iki katından fazla olacağı anlamına gelir. Fakat pi sayısının iki katı oranından sapma, özellikle de c’de bulunan büyük değer, tam da dönen Tornado’da bulduğumuz sonuçtur. Bu da Einstein’ı “olağanın”, başka bir deyişle Eukleidesçi geometrinin çiğnenmesini açıklamaya yönelik bir fikir ileri sürmeye götürdü: Uzayın eğrilmesi. Yunanlıların, binlerce yıldır okullarda çocuklara öğretilen geometrisi Tornado’da dönen biri için geçerli olmuyordu işte. Onun yerini c’de şematik olarak çizilmiş kıvrımlı uzay genellemesi alıyordu.
Böylece Einstein, Yunanlıların kanunlaştırmış olduğu, bildik geometrik uzamsal ilişkilerin, düz bir masa üzerindeki bir daire gibi “düz” uzam şekilleri için geçerli olan ilişkilerin, ivmeli bir gözlemcinin bakış açısı söz konusu olduğunda geçerli olmadığını fark etmişti. Burada ivmeli hareketin yalnızca bir biçimini inceledik, ama Einstein aynı sonucun –uzayın yamulmasının- bütün ivmeli hareket biçimleri için geçerli olduğunu göstermişti.
Aslına bakarsanız ivmeli hareket sadece uzayın yamulmasına değil, benzer bir biçimde zamanın da yamulmasına yol açar. (Kronolojik olarak Einstein önce zamanın yamulmasına odaklanmış, uzayın yamulmasının önemini bundan sonra ayrımsamıştı.) Bir bakıma, zamanın da etkileniyor olması çok da şaşırtıcı gelmemeli, özel göreliliğin uzay ile zaman arasında bir birlikteliği ifade ettiğini II.Bölüm’de görmüştük. Bu birleşme, 1908’de özel görelilik ile ilgili bir konferansta, Minkowski’nin şairane sözleriyle şöyle özetlenmişti: “Bundan böyle kendi başına uzay, kendi başına zaman, gölgeler arasında kaybolup gidecek, sadece ikisinin bir birliği bağımsızlığını koruyacak.” Özel görelilik kuramı da daha gerçekçi, fakat aynı ölçüde muğlak bir dille, uzay ile zamanı uzay-zamanın birleşik yapısı içinde bir araya getirerek “Uzay için geçerli olan zaman için de geçerlidir,” der. Fakat bu bir soru doğuruyor: Yamulmuş uzayı, eğri bir şekilde resmedebiliyoruz, peki ya yamulmuş zaman derken aslında neyi kast ediyoruz?
Cevabı biraz kestirebilmek için Slim ile Jim’i yine Tornado’ya bindirelim ve onlardan şu deneyi gerçekleştirmelerini isteyelim; Slim, Tornado’nun ortasından geçen kirişlerden birinin ucunda, sırtını pleksiglasın iç yüzüne vererek duracak, Jim de merkezden başlayarak kiriş boyunca yavaş yavaş ona doğru emekleyecek. Birkaç adımda bir Jim duracak ve iki kardeş saatlerini karşılaştıracaklar. Ne görecekler? Yukarıdan, sabit yerimizden onları izlerken cevabı tahmin edebiliriz yine: Saatleri tutmayacak. Bu sonuca varıyoruz, çünkü Slim ile Jim’in farklı hızlarda yol aldığının farkındayız; Tornado’da bir kiriş üzerinde merkezden uzaklaştıkça, bir dönüşü tamamlamak için daha çok yol alırsınız, dolayısıyla da daha hızlı gidersiniz. Fakat özel göreliliğe göre, ne kadar hızlı giderseniz saatiniz o kadar yavaş ilerler, buradan da Slim’in saatinin Jim’in saatinden daha yavaş işleyeceğini anlıyoruz. Dahası Slim ile Jim, Jim Slim’e yaklaştıkça Jim’in saatinin yavaşladığını, Slim’in saatinin hızına yaklaştığını da görecek. Bu da, Jim’in kiriş üzerinde merkezden uzağa gittikçe, dairesel hızının artıp Slim’inkine yaklaşacağını yansıtıyor.
Slim ile Jim gibi, Tornado’daki gözlemciler açısından, zamanın akış hızının, tam olarak durdukları yere –bu durumda Tornado’nun merkezinden uzaklıklarına- bağlı olduğu sonucuna varıyoruz. İşte bu, yamulmuş zamanla ne kast ettiğimizi gösterir: Akış hızı bir yerden diğerine farklılık gösteriyorsa, zaman yamulmuştur. Buradaki tartışmamız açısından özellikle önemli bir nokta daha var. Jim kiriş üzerinde emeklerken bir şeyi daha fark edecektir. Dışa doğru giderek daha güçlü bir biçimde çekildiğini hissedecektir, çünkü Tornado’nun merkezinden uzaklaştıkça yalnızca hızı artmakla kalmamış, ivmesi de artmıştır. O halde Tornado’da, ivmenin artmasının saatlerin yavaşlamasıyla bağlantılı olduğunu, yani ivme arttıkça bunun zamanda daha önemli bir yamulmaya yol açtığını görüyoruz.
Bu gözlemler Einstein’ı nihai adıma götürdü. Kütleçekimi ile ivmeli hareketin gerçekte birbirinden ayırt edilemez olduğunu daha önce göstermişti, şimdi de ivmeli hareketin uzay ve zamanın yamulmasıyla ilgili olduğunu gösteriyordu; böylece kütleçekiminin “kara kutusunun” içindekilere, yani kütleçekiminin işleyiş mekanizmasına ilişkin şu önermeyi ortaya attı: Kütleçekimi (Einstein’a göre) uzay ile zamanın yamulmasıdır.
Kaynak : Evrenin Zarafeti - Brian Greene